Алгоритмы, которые вы должны знать перед System Design Interview
В этой статье рассмотрим алгоритмы: Geohashing, Quadtree, Consistent hashing, Leaky Bucket, Token Bucket и Trie, которые смогут вам пригодиться на собеседовании по System design
Geohashing
Что такое геохеширование?
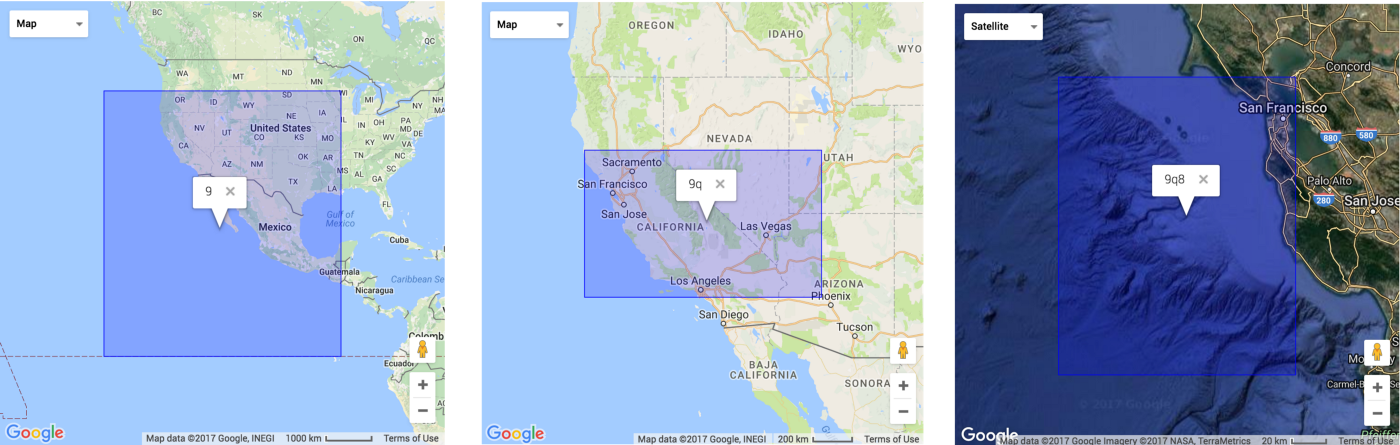
Geohash — это система геокодирования, изобретенная Густаво Нимейером, которая позволяет нам узнать, в какой области карты находится пользователь.
Широта и долгота представляют только одну точку на карте, а геохеш описывает фиксированную область, что более гибко и удобно для сервисов поиска в заданной области. Геохеширование также можно использовать для обеспечения анонимности, поскольку не нужно раскрывать точное местоположение пользователя, в зависимости от длины гео-хеша мы просто знаем, что он находится где-то в пределах области.
Мы также можем использовать это, чтобы узнать, когда 2 пользователя находятся близко друг к другу, давайте рассмотрим этих 2 пользователей, показанных ниже, каждый из которых представлен 9-значным гео-хешем. Девять цифр очень точно позволяют нам узнать, что они находятся где-то в пределах 5 метрового квадрата.
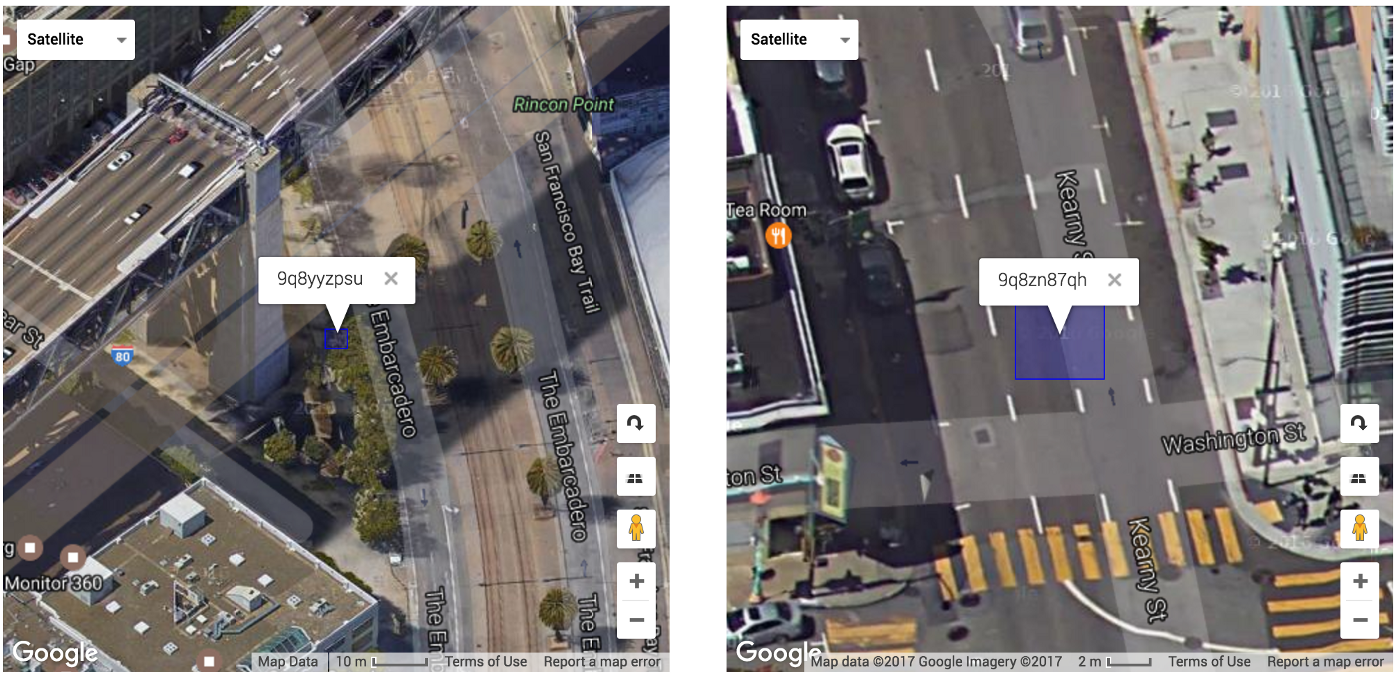
Эти 2 пользователя находятся в зоне «9q8» , один в « 9q8y», а другой в « 9q8z».
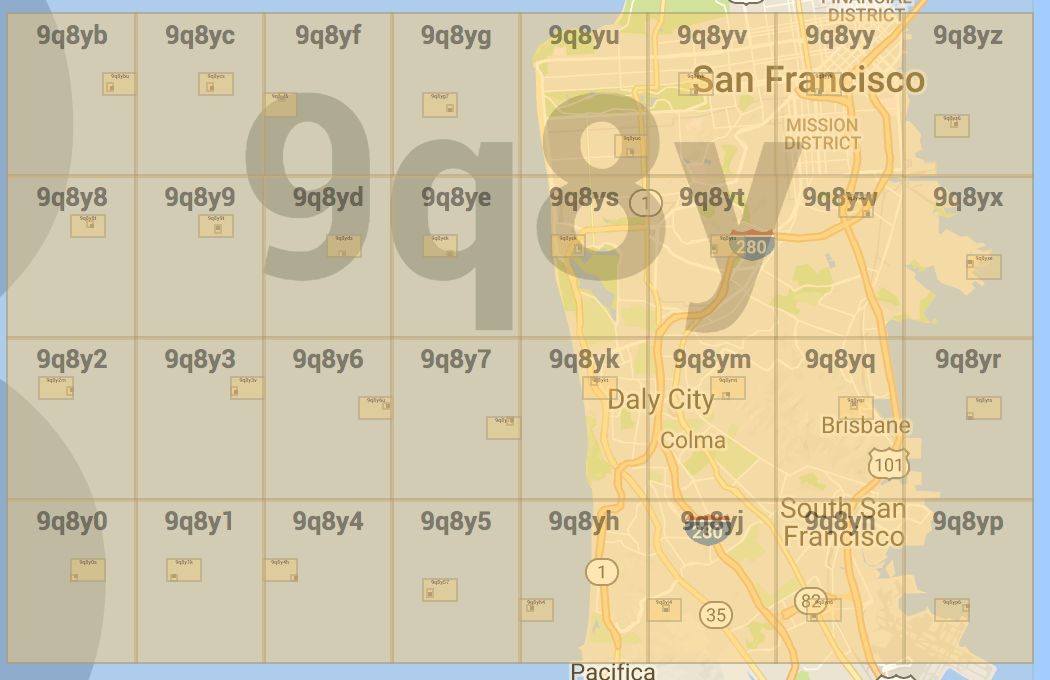
Посмотреть разбивку секций GeoHash на карте мира можно здесь.
Как переобразовать локацию пользователя в геохеш?
Уже cуществуют готовые пакеты которые это делают, например: latlon-geohash
Quadtree
Что такое Quadtree?
Давайте рассмотрим этот алгоритм на примере: поиск ближайших ресторанов в Yelp или Google map.
Quadtree -- это структура данных, которая обычно используется для разбиения двумерного пространства путем рекурсивного разделения его на четыре квадранта (сетки) до тех пор, пока содержимое сеток не будет соответствовать определенным критериям (см. картинку ниже).
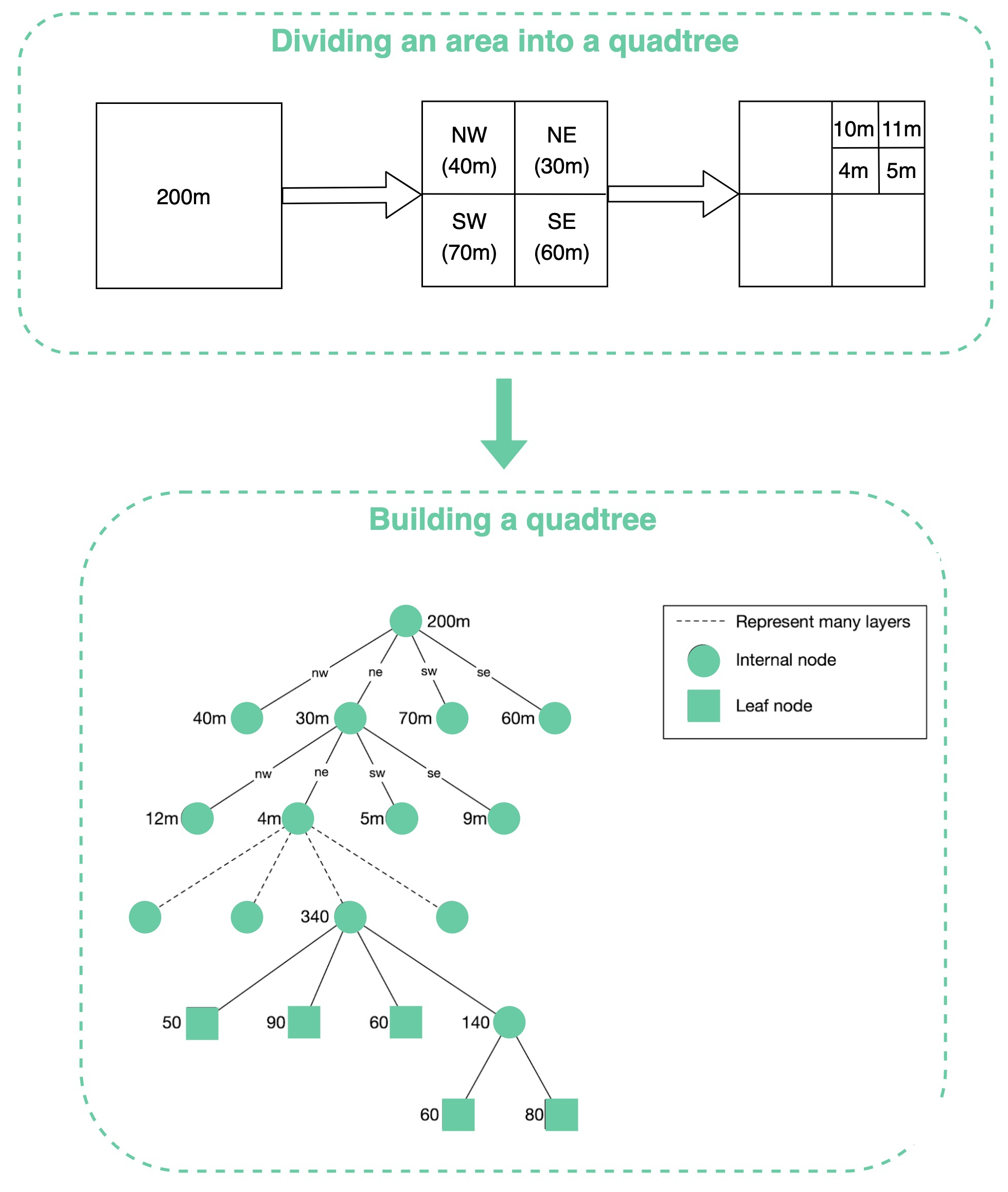
Quadtree это in-memory data structure, а не решение для базы данных. Он работает на каждом сервере LBS (Location-Based Service) и структура данных создается во время запуска сервера.
Complexity
- Time complexity:
- Find: O(log2N)
- Insert: O(log2N)
- Search: O(log2N)
- Space complexity: O(k log2N)
Consistent hashing
Согласованное хеширование используется в распределенных системах, чтобы хеш-таблица не зависела от количества доступных серверов, чтобы свести к минимуму перемещение ключей при изменении масштаба.
Давайте для начала вспомним, что такое хеширование и для чего оно используется:
В классическом подходе к хешированию используется хеш-функция для генерации псевдослучайного числа, которое затем делится на размер пространства памяти для преобразования случайного идентификатора в позицию в доступном пространстве, Это используется например в таких дата структурах как Dictionary. Схематически это выглядит следующим образом:
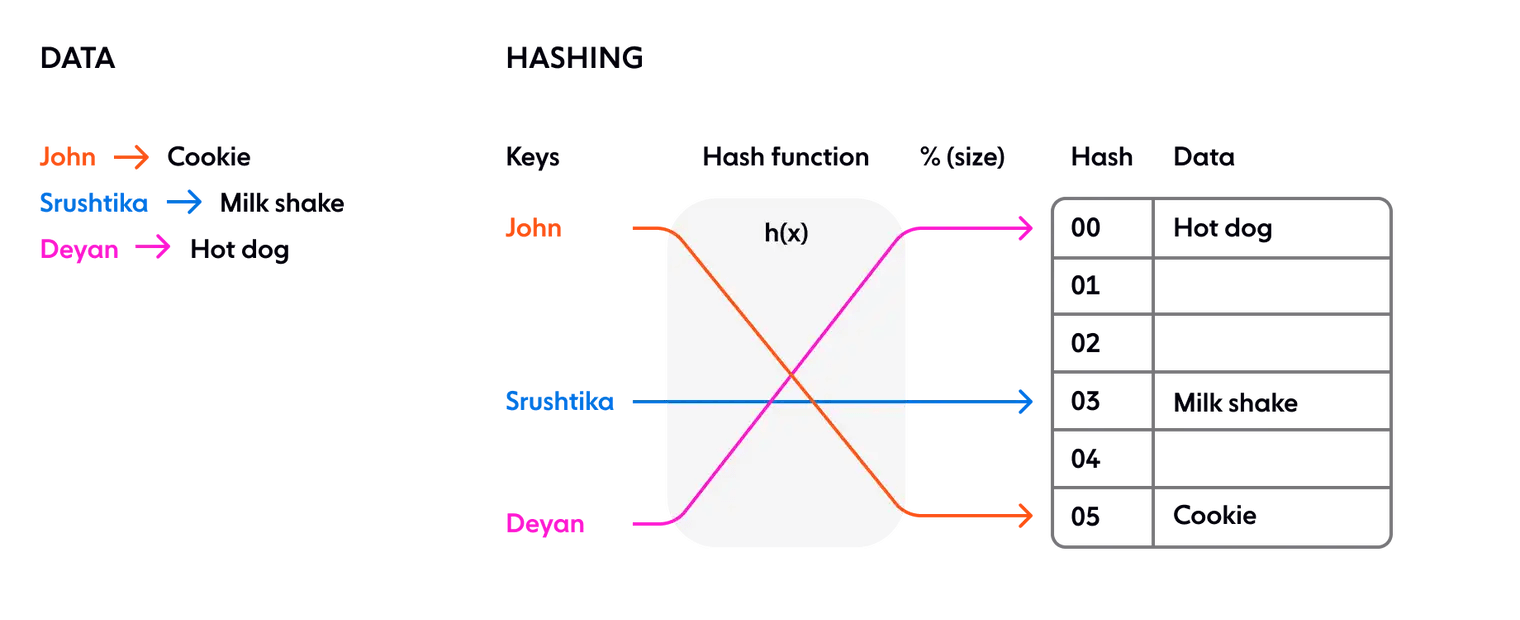
Хеширование в распределенной системе
В сценарии, когда различные источники делают реквесты с нескольких нод серверов, нам нужен механизм для равномерного сопоставления запросов с доступными серверными нодами, что обеспечивает балансировку нагрузки для стабильной производительности.
В классическом методе хеширования мы всегда предполагаем, что:
- Количество ячеек памяти известно
- Это количество никогда не меняется
Кластер обычно скейлиться вверх и вниз, и в распределенной системе всегда случаются неожиданные сбои. Мы не можем гарантировать, что количество нод сервера останется прежним. А если один из них выйдет из строя? При наивном подходе к хешированию нам нужно перехешировать каждый отдельный ключ, поскольку новое сопоставление зависит от количества нод и областей памяти, как показано ниже:
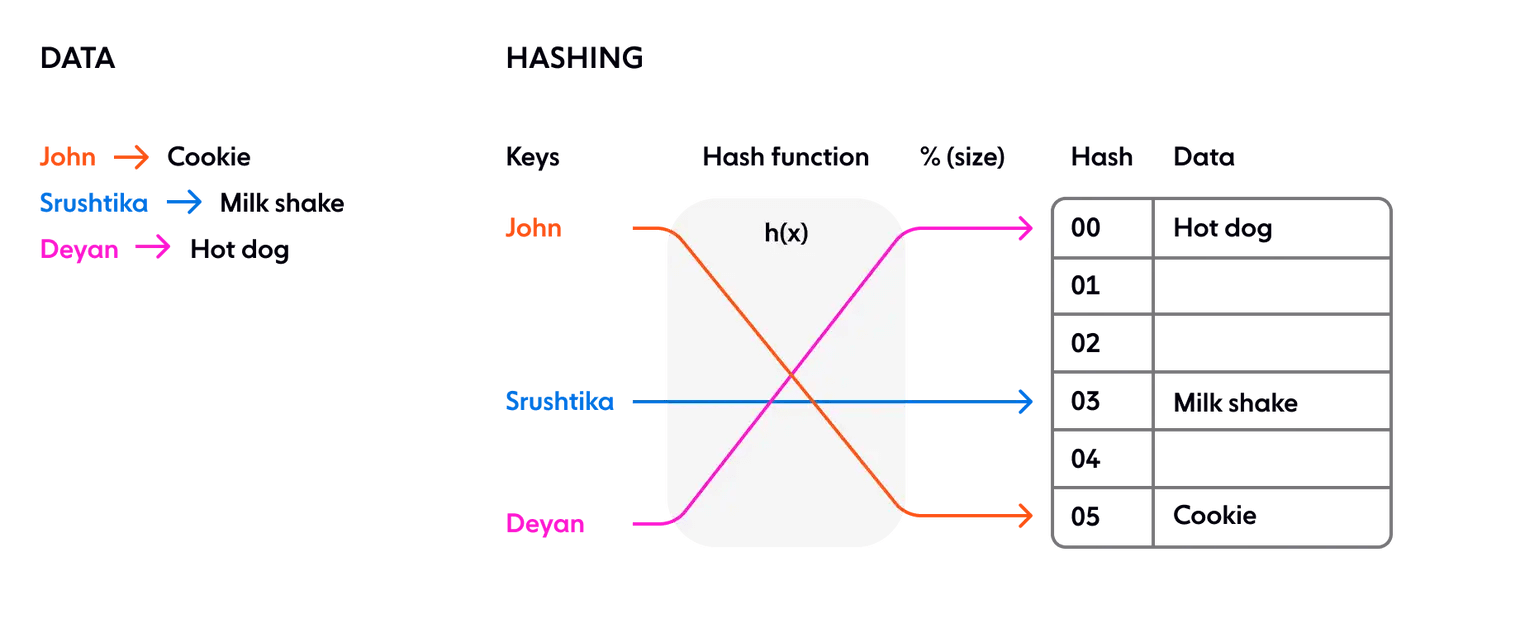
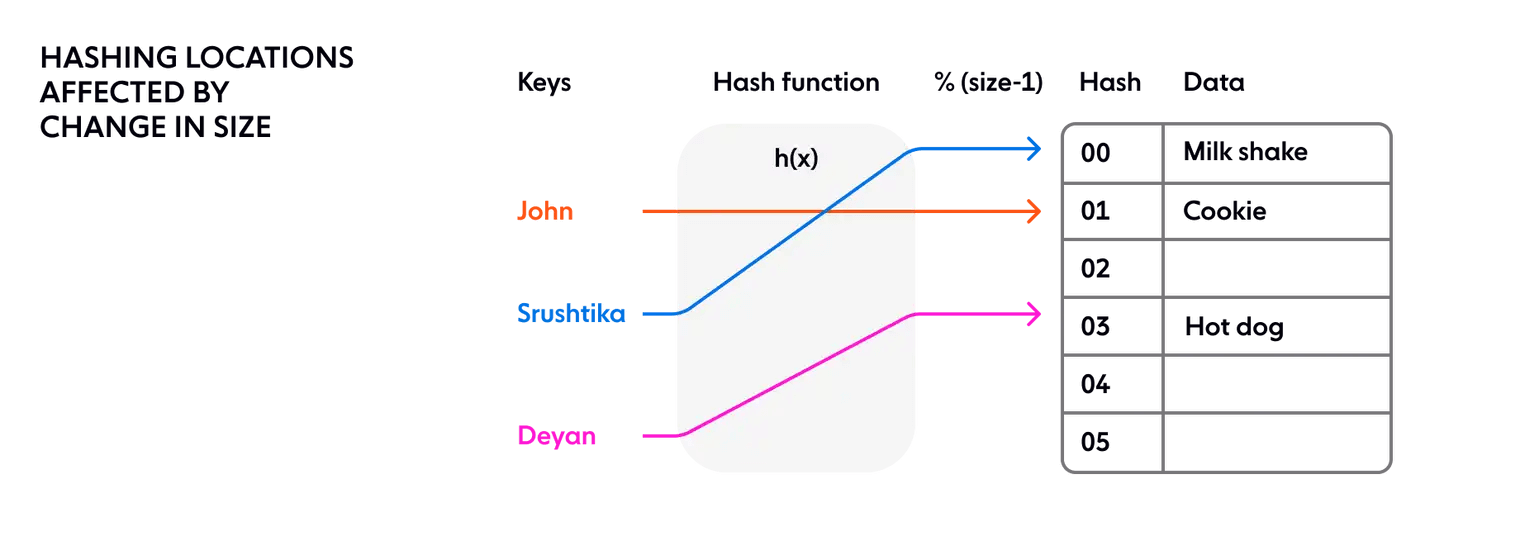
В чем проблема в распределенной системе с перехешированием? Перемещение размещения каждого ключа — заключается в том, что состояние сохраняется на каждой ноде. Изменение размера кластера может привести к перетасовке данных в кластере. По мере роста размера кластера это становится неустойчивым, поскольку объем работы, необходимой для каждого изменения хэша, растет линейно с размером кластера.
Вот тут нам и поможет концепция Consistent hashing
Что такое Consistent hashing?
Consistent hashing можно описать следующим образом:
- Он представляет resource requestors (которые мы будем ниже называть «запросами») и серверные ноды в структуре виртуального кольца, известной как хеширование.
- Количество локаций больше не фиксировано, но считается, что кольцо имеет бесконечное количество точек, и серверные узлы могут быть размещены в произвольном месте этого кольца. (Конечно, снова выбрать это случайное число можно с помощью хеш-функции, но второй шаг деления его на количество доступных местоположений пропускается, так как это уже не конечное число).
- Запросы, то есть пользователи, компьютеры или serverless функции, которые аналогичны ключам в классическом подходе к хешированию, также размещаются в том же кольце с использованием той же хеш-функции.
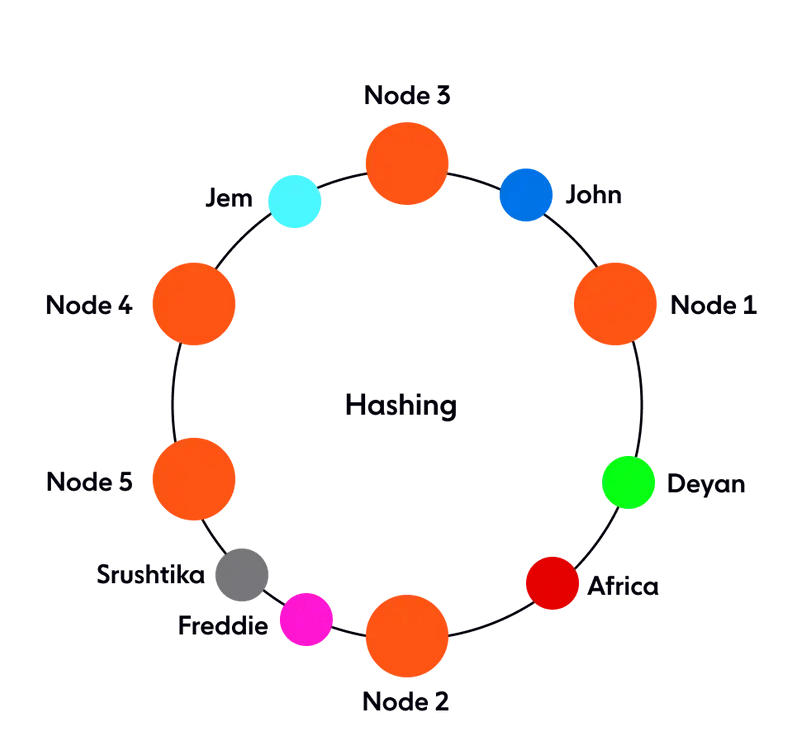
Как принимается решение о том, какой запрос будет обслуживаться той или иной Nod'ой? Если мы предположим, что кольцо упорядочено так, что обход кольца по часовой стрелке соответствует порядку расположению адресов, каждый запрос может быть обслужен узлом сервера, который первым появляется в этом обходе по часовой стрелке.
То есть первая нода с адресом больше адреса запроса получает его обслуживание. Если адрес запроса выше, чем у узла с наивысшим адресом, он обслуживается узлом сервера с наименьшим адресом, поскольку обход по кольцу идет по кругу (смотрите картинку ниже):
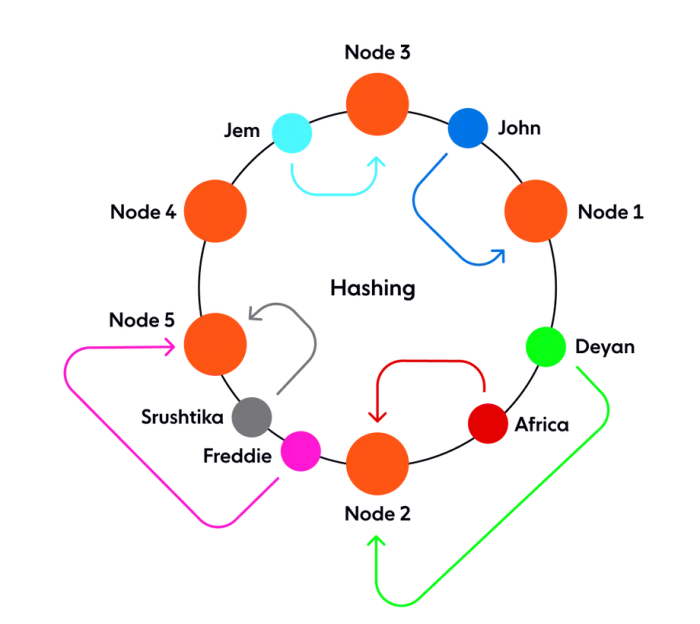
Теоретически каждая нода«владеет» диапазоном хеширования, и любые запросы, поступающие в этот диапазон, будут обслуживаться одной нодой.
Как работает consistent hashing?
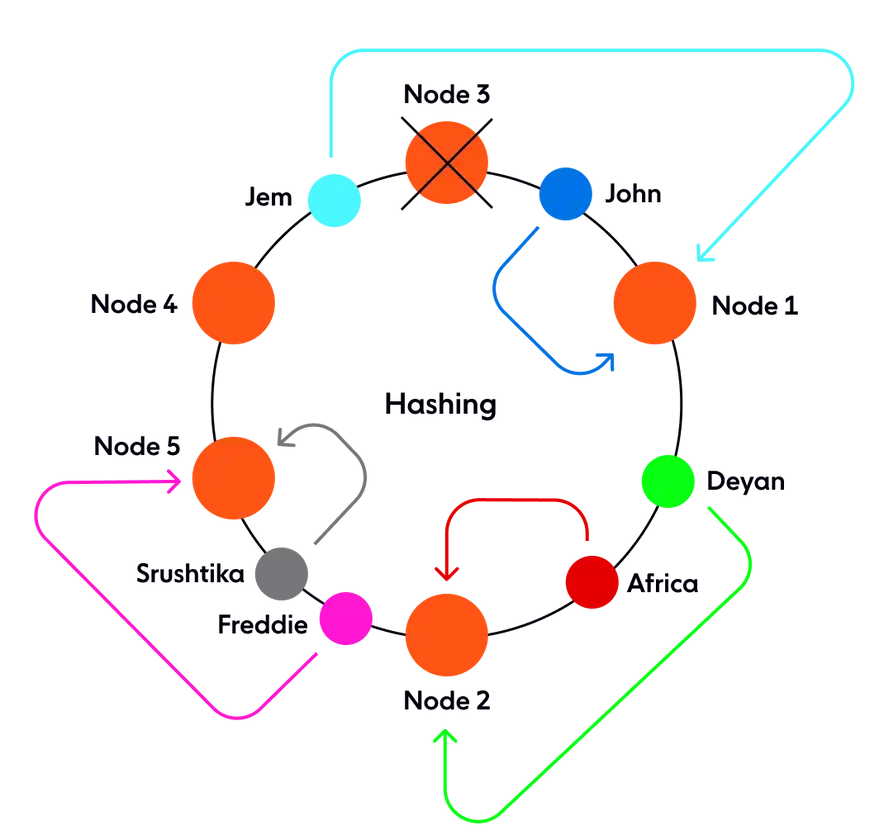
Теперь, что если одна из нод выходит из строя, скажем, node 3, диапазон следующей ноды расширяется, и любой запрос, поступающий во всем этом диапазоне, направляется на новую ноду. Но это все. Только этот диапазон, соответствующий вышедшему из строя, необходимо было переназначить, в то время как остальные назначения нод хеширования и запроса остаются неизменными.
Leaky Bucket (протекающее ведро)
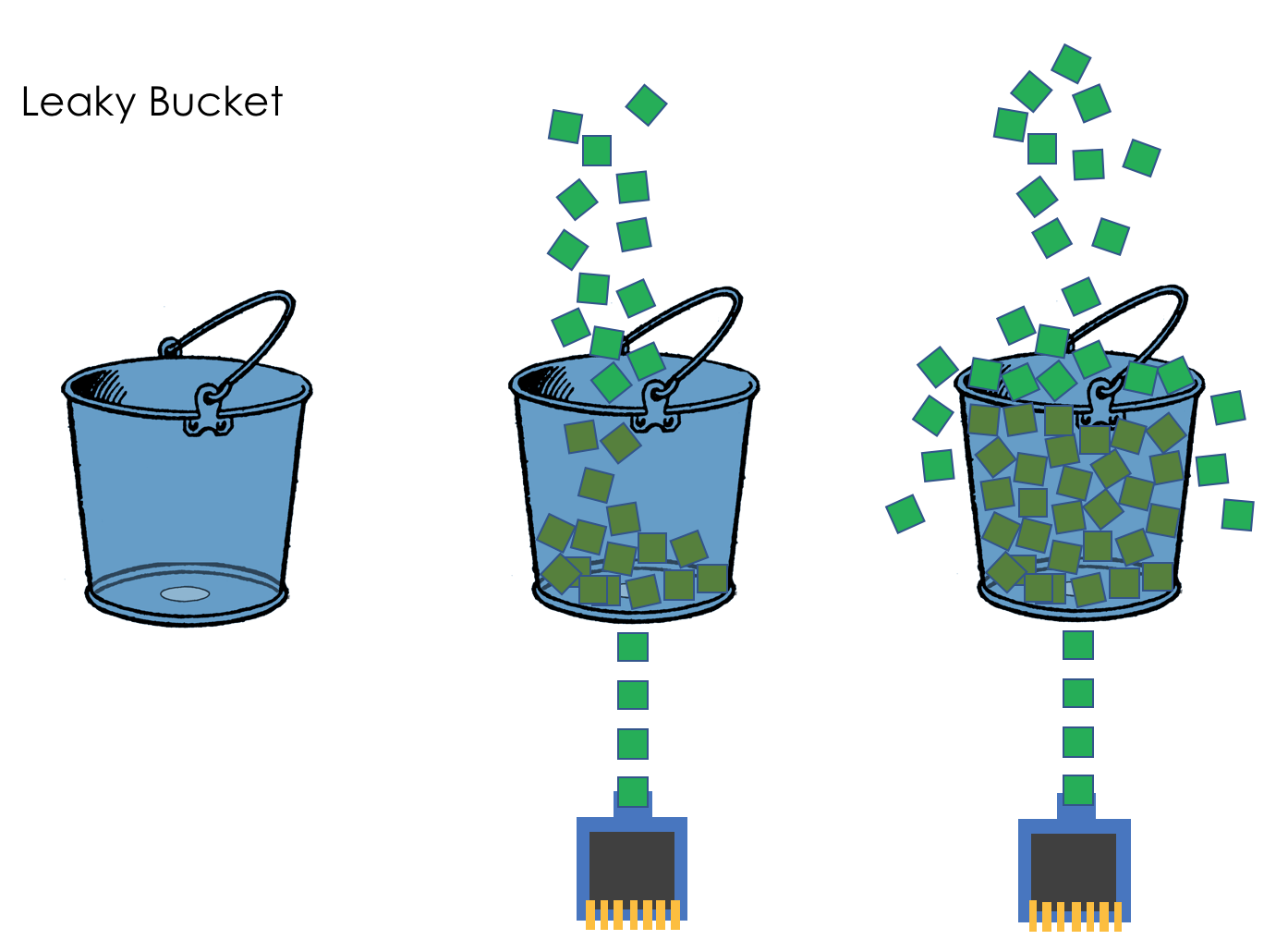
Leaky Bucket — это алгоритм, который обеспечивает наиболее простой, интуитивно понятный подход к ограничению скорости обработки при помощи очереди, которую можно представить в виде «ведра» содержащего запросы. Когда запрос получен, он добавляется в конец очереди. Через равные промежутки времени первый элемент в очереди обрабатывается. Это также известно как очередь FIFO. Если очередь заполнена, то дополнительные запросы отбрасываются (или “утекают”).
Преимущество данного алгоритма состоит в том, что он сглаживает всплески и обрабатывает запросы примерно с одной скоростью, его легко внедрить на одном сервере или балансировщике нагрузки, он эффективен по использованию памяти, так как размер очереди для каждого пользователя ограничен.
Однако при резком увеличении трафика очередь может заполниться старыми запросами и лишить систему возможности обрабатывать более свежие запросы. Также он не дает гарантии, что запросы будут обработаны за какое-то фиксированное время. Кроме того, если для обеспечения отказоустойчивости или увеличения пропускной способности вы загружаете балансировщики, то вы должны реализовать политику координации и обеспечения глобального ограничения между ними.
Существует разновидность данного алгоритма — Token Bucket («ведро с токенами» или «алгоритм маркерной корзины»).
Token Bucket
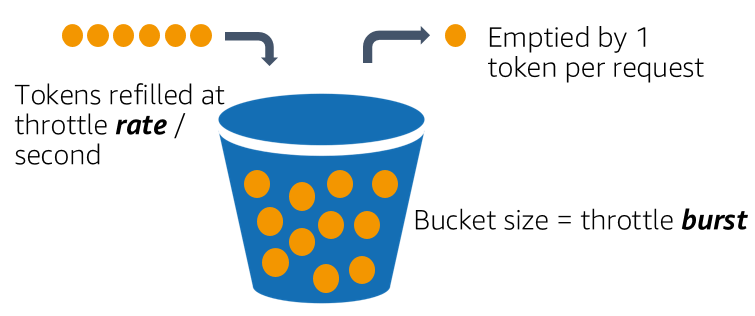
Существуют вариации с использованием нескольких «вёдер», при этом как размеры, так и скорость поступления токенов в них могут быть разными у отдельных «вёдер». Если в первом «ведре» токенов для обработки запроса недостаточно, то проверяется их наличие во втором и т.д., но при этом приоритет обработки запроса понижается (как правило, это используется при проектировании сетевых интерфейсов, когда можно, например, изменить значение поля DSCP обрабатываемого пакета).
Ключевым отличием от реализации Leaky Bucket является то, что токены могут накопиться при простое системы, и дальше может случиться burst нагрузки, при этом запросы будут обработаны (т.к. имеется достаточное количество токенов), в то время как Leaky Bucket гарантированно будет сглаживать нагрузку даже в случае простоя.
Trie алгоритм (нагруженное дерево, префиксное дерево)
Зачем используется Trie?
Нагруженное дерево — структура данных реализующая интерфейс ассоциативного массива, то есть позволяющая хранить пары «ключ-значение». Сразу следует оговориться, что в большинстве случаев ключами выступают строки, однако в качестве ключей можно использовать любые типы данных, представимые как последовательность байт.
Область применения нагруженных деревьев: их можно применять везде где требуется реализация интерфейса ассоциативного массива. Особенно нагруженные деревья удобны для реализации словарей, спеллчекеров и прочих Т9 — то есть в задачах, где необходимо быстро получать наборы ключей с заданным префиксом. Также нагруженное дерево использует в своей работе алгоритм Ахо — Корасик.
Принцип работы Trie алгоритма
Нагруженное дерево отличается от обычных n-арных деревьев тем, что в его узлах не хранятся ключи. Вместо них в узлах хранятся односимвольные метки, а ключем, который соответствует некоему узлу является путь от корня дерева до этого узла, а точнее строка составленная из меток узлов, повстречавшихся на этом пути. В таком случае корень дерева, очевидно, соответствует пустому ключу.
На рисунке вы можете наблюдать пример нагруженного дерева с ключами c, cap, car, cdr, go, if, is, it.
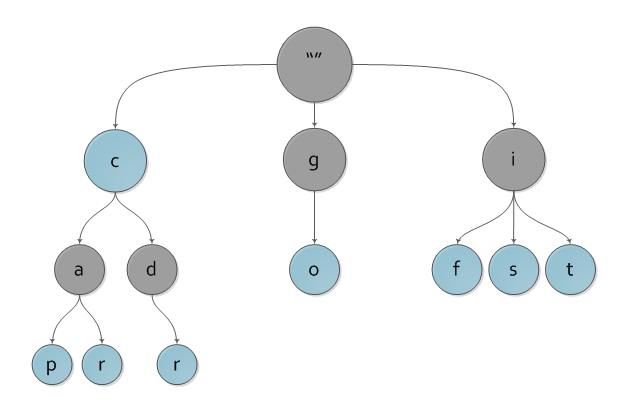
И то же самое дерево с выделенным на нем ключем car.
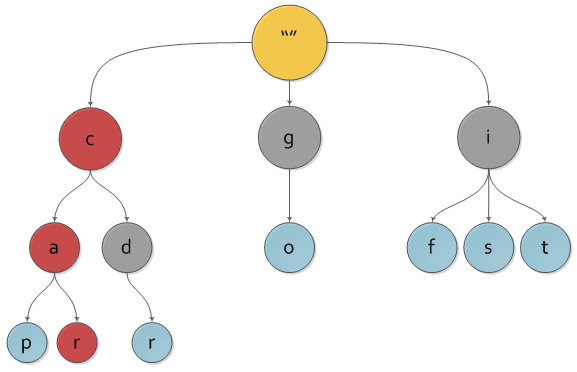
Сразу видно, что наше дерево содержит «лишние» ключи, ведь любому узлу дерева соответствует единственный путь до него от корня, а значит и некоторый ключ. Чтобы избежать проблемы с «лишними» ключами, каждому узлу дерева добавляется булева характеристика, указывающая, является ли узел реально существующим либо промежуточным по дороге в какой-либо другой.
Поиск ключа в Trie
Пусть дан ключ Key, который нужно найти в дереве. Будем спускаться из корня дерева на нижние уровни, каждый раз переходя в узел, чья метка совпадает с очередным символом ключа. После того как обработаны все символы ключа, узел, в котором остановился спуск и будет искомым узлом. Если в процессе спуска не нашлось узла с меткой, соответствующей очередному символу ключа, или спуск остановился на промежуточной вершине (вершине, не имеющей значения), то искомый ключ отсутствует в дереве.
Временная сложность этого алгоритма равна О(|Key|). Схематически поиск будет выглядить следующим образом:
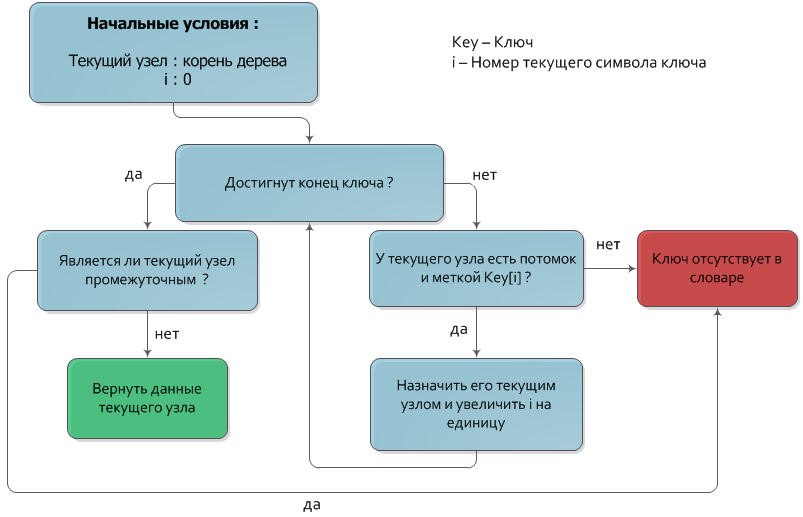
Вставка ключа в Trie
Алгоритм добавления ключа в дерево очень похож на алгоритм поиска.
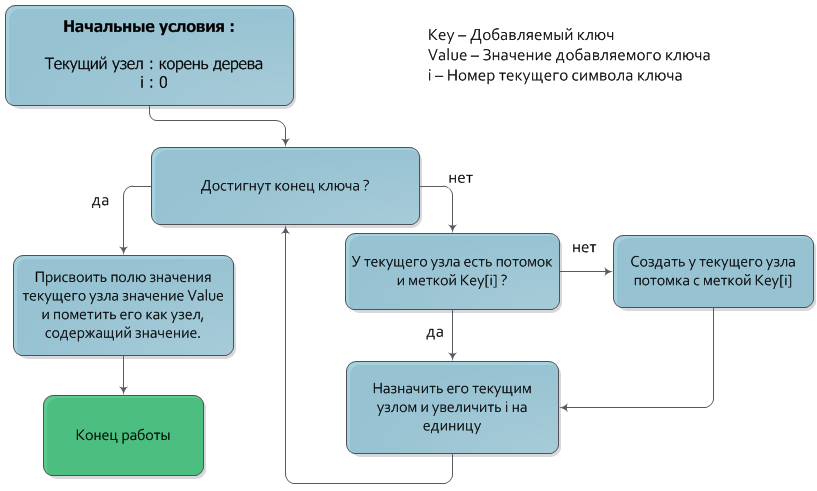
Пусть дана пара из ключа Key и значения Value, которую нужно добавить. Как и в алгоритме поиска ключа, будем спускаться из корня дерева на нижние уровни, каждый раз переходя в узел, чья метка совпадает с очередным символом ключа. После того как обработаны все символы ключа, узел, в котором остановился спуск и будет узлом, которому должно быть присвоено значение Value (также, разумеется, узел должен быть помечен как имеющий значение). Если в процессе спуска отсутствует узел с меткой, соответствующей очередному символу ключа, то следует создать новый промежуточный узел с нужной меткой и назначить его потомком текущего.
Временная сложность добавления ключа — О(|Key|).
Удаление ключа в Trie
Удаление ключа также реализуется очень легко.
Пусть дан ключ Key, который необходимо удалить из дерева. Проведем поиск этого ключа. Если ключ в словаре, то зная узел, которому он соответствует, можно просто пометить его как промежуточный, сделав его «невидимым» для последующих поисков.
После этого можно подняться от «отключенного» узла к корню, попутно удаляя все узлы которые являются листьями, однако экономия памяти в данном случае не существенна, а для эффективного определения того, является ли узел листом потребуется вводить дополнительную характеристику узла.
Временная оценка алгоритма удаления — знакомое уже О(|Key|).
